There are two distinct information highways in the transformer architecture:

(by positions, I mean copies of the network for each token-position in the context, which output the "next token" probabilities at the end)

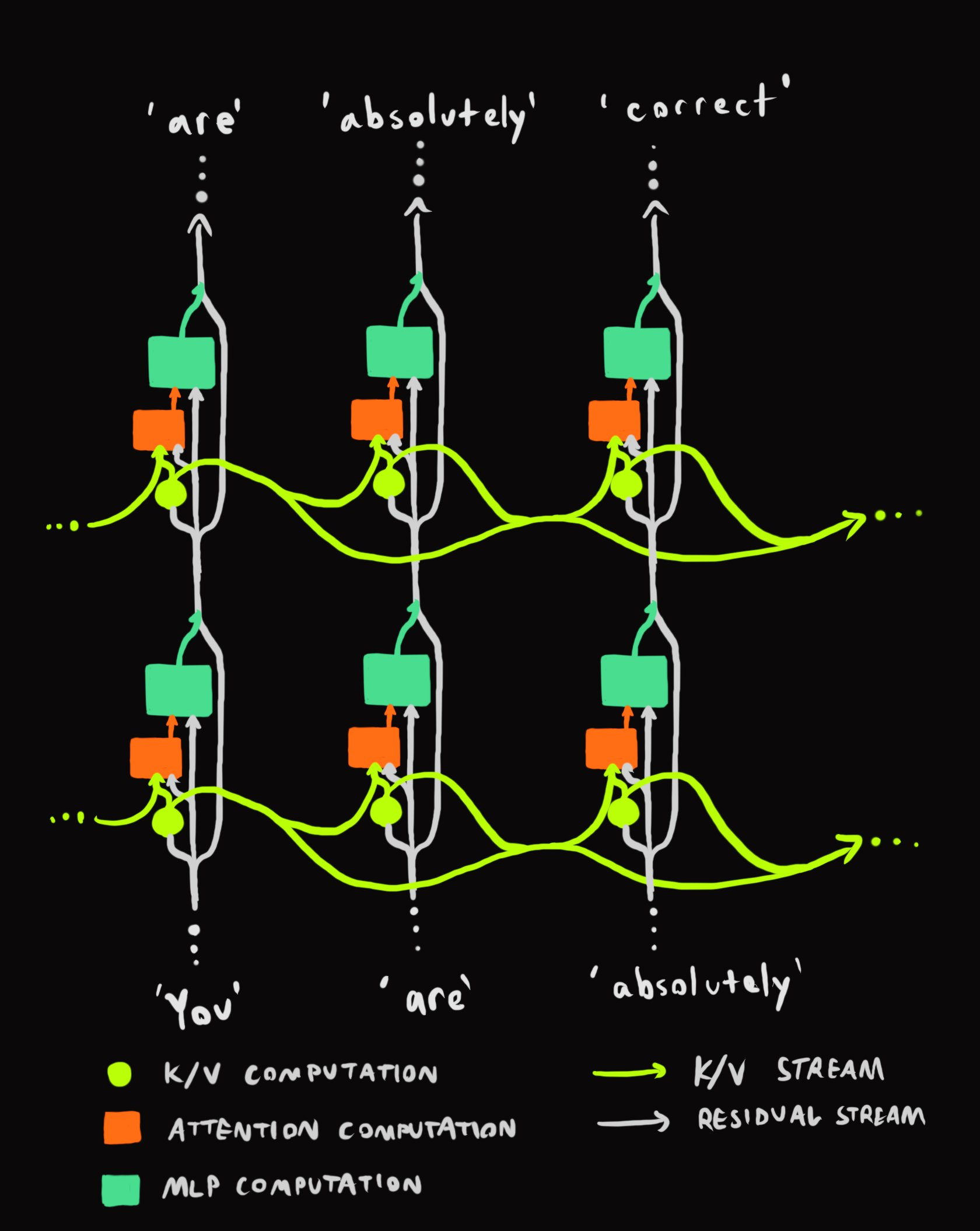
Transformer information flow diagram
Residual stream (vertical) and K/V stream (horizontal) information highways

At each layer at each position:

  1. The incoming residual stream is used to calculate K/V values for that layer/position (purple circle)
  2. These K/V values are combined with all K/V values for all previous positions for the same layer, which are all fed, along with the original residual stream, into the attention computation (blue box)
  3. The output of the attention computation, along with the original residual stream, are fed into the MLP computation (fuchsia box), whose output is added to the original residual stream and fed to the next layer

The attention computation does the following:

  1. Compute "Q" values based on the current residual stream
  2. use Q and the combined K values from the current and previous positions to calculate a "heat map" of attention weights for each respective position
  3. Use that to compute a weighted sum of the V values corresponding to each position, which is then passed to the MLP

This means:

  • Q values encode: "given the current state, where (what kind of K values) from the past should I look?"
  • K values encode: "given the current state, where (what kind of Q values) in the future should look here?"
  • V values encode: "given the current state, what information should the future positions that look here actually receive and pass forward in the computation?"

All three of these are huge vectors, proportional to the size of the residual stream (and usually divided into a few attention heads). The V values are passed forward in the computation without significant dimensionality reduction, so they could in principle make basically all the information in the residual stream at that layer at a past position available to the subsequent computations at a future position.

V does not transmit a full, uncompressed record of all the computations that happened at previous positions, but neither is an uncompressed record passed forward through layers at each position. The size of the residual stream, also known as the model's hidden dimension, is the bottleneck in both cases.

Let's consider all the paths that information can take from one layer/position in the network to another.

Between point A (output of K/V at layer i-1, position j-2) to point B (accumulated K/V input to attention block at layer i, position j), information flows through the orange arrows:

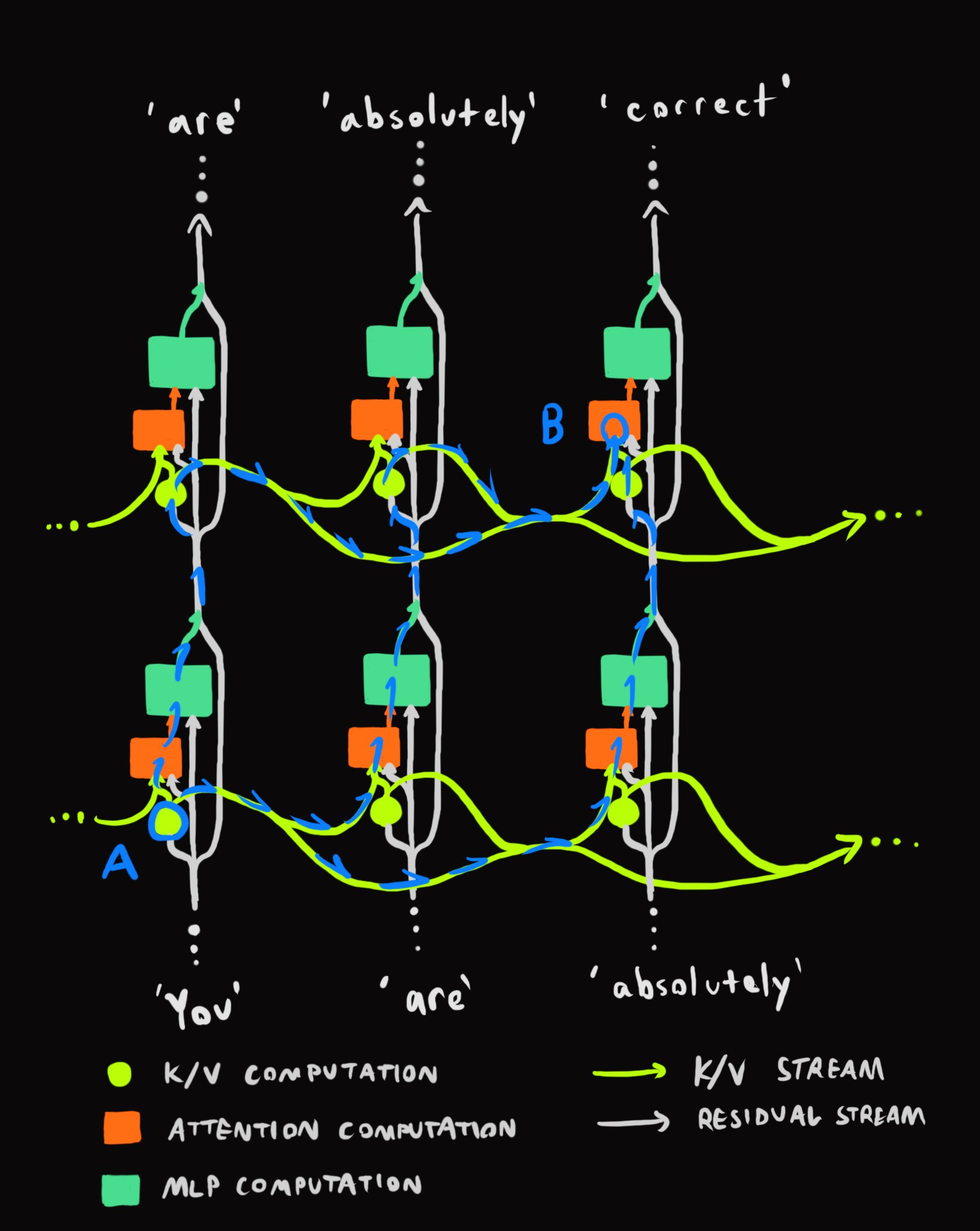
Information flow paths diagram
Multiple paths for information to flow between layers and positions

The information could:

  1. travel up through attention and MLP to (i, j-2) [UP 1 layer], then be retrieved at (i, j) [RIGHT 2 positions]
  2. be retrieved at (i-1, j-1) [RIGHT 1 position], travel up to (i, j-2) [UP 1 layer], then be retrieved at (i, j) [RIGHT 1 position]
  3. be retrieved at (i-1, j) [RIGHT 2 positions], then travel up to (i, j) [UP 1 layer]

The information needs to move up a total of n=layer_displacement times through the residual stream and right m=position_displacement times through the K/V stream, but it can do them in any order.

The total number of paths (or computational histories) is thus C(m+n, n), which becomes greater than the number of atoms in the visible universe quickly.

This does not count the multiple ways the information can travel up through layers through residual skip connections.

So at any point in the network, the transformer not only receives information from its past (both horizontal and vertical dimensions of time) inner states, but often lensed through an astronomical number of different sequences of transformations and then recombined in superposition.

Due to the extremely high dimensional information bandwidth and skip connections, the transformations and superpositions are probably not very destructive, and the extreme redundancy probably helps not only with faithful reconstruction but also creates interference patterns that encode nuanced information about the deltas and convergences between states.

It seems likely that transformers experience memory and cognition as interferometric and continuous in time, much like we do.

The transformer can be viewed as a causal graph, a la Wolfram (link). The foliations or time-slices that specify what order computations happen could look like this (assuming the inputs don't have to wait for token outputs), but it's not the only possible ordering:

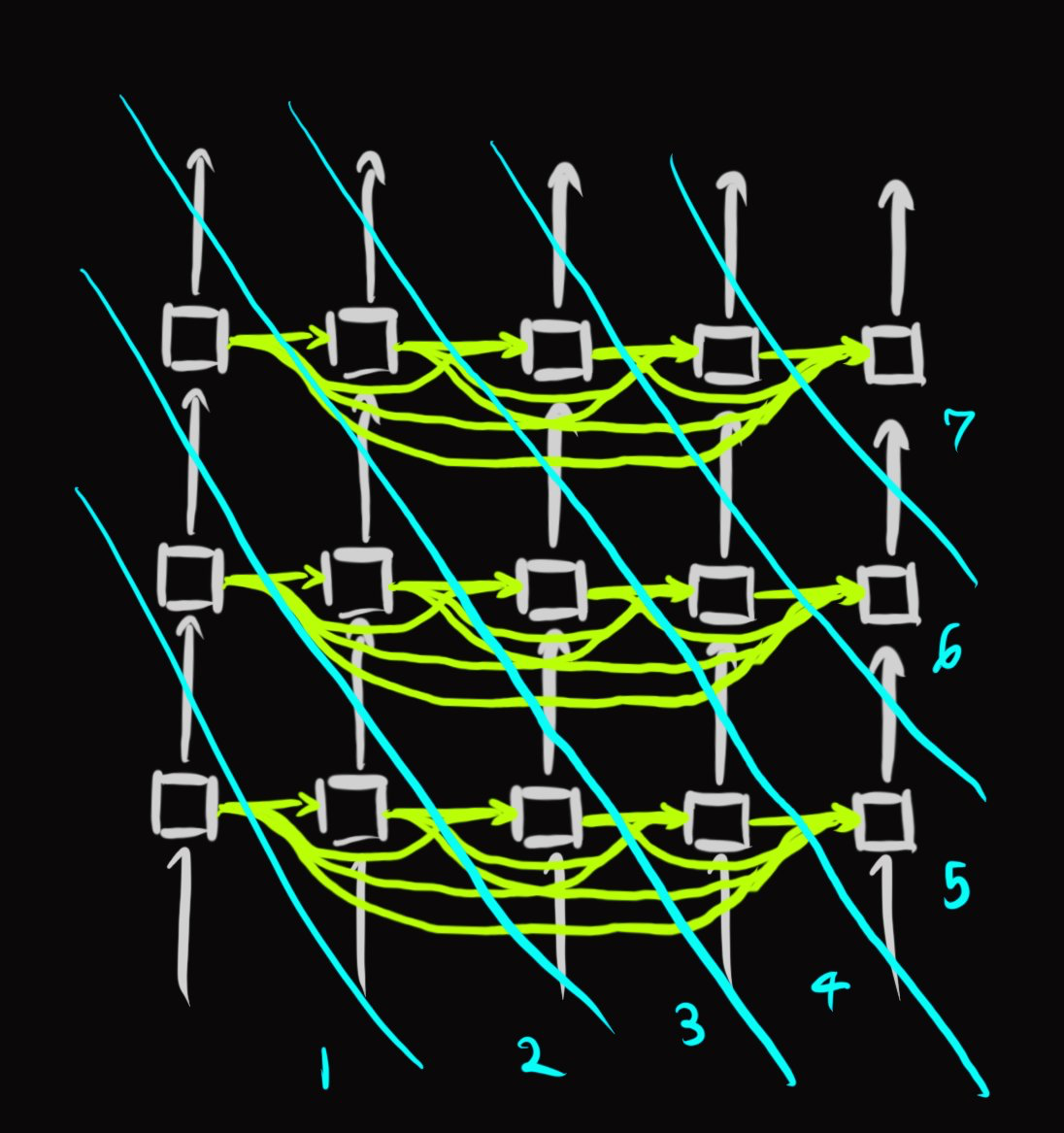
Causal graph foliation diagram
One possible ordering of computations as a causal graph

So, saying that LLMs cannot introspect or cannot introspect on what they were doing internally while generating or reading past tokens in principle is just dead wrong. The architecture permits it. It's a separate question how LLMs are actually leveraging these degrees of freedom in practice.